3.1.- Representación De Objetos En Tres Dimensiones.
En computación, un modelo en 3D es un "mundo conceptual en tres dimensiones".Un modelo 3D puede "verse" de dos formas distintas. Desde un punto de vista técnico, es un grupo de fórmulas matemáticas que describen un "mundo" en tres dimensiones.
Desde un punto de vista visual, valga la redundancia, un modelo en 3D es un representación esquemática visible a través de un conjunto de objetos, elementos y propiedades que, una vez procesados (renderización), se convertirán en una imagen en 3D o una animación 3d.
Representacion Grafica
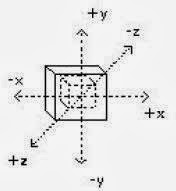
La representación de los objetos en tres dimensiones sobre una superficie plana, de manera que ofrezcan una sensación de volumen se llama Perspectiva. Se representan los objetos sobre tres ejes XYZ. En el eje Z, se representa la altura. En el eje Y, se representa la anchura y en el eje X, se representa la longitud. Los distintos tipos de perspectivas dependen de la inclinación de los planos Los sistema más utilizados son la isométrica, la caballera y la cónica. Estudiaremos en este curso las dos primeras.
Perspectiva Isométrica.- En ella los ejes quedan separados por un mismo ángulo (120º). Las medidas siempre se refieren a los tres ejes que tienen su origen en un único punto.
Dibujar en perspectiva
En ambas perspectivas, el sistema más sencillo es llevar las tres vistas principales sobre los planos formados por los ejes:
- Alzado en el plano XZ.
- Planta en el plano XY.
- Perfil en el plano YZ.
Cada una de las aristas que forman las vistas se prolonga paralelamente al eje que corresponda:
- Horizontal paralelo al eje de las X.
- Vertical paralelo al eje de las Z.
- Profundidad paralelo al eje de las Y.
3.2 Visualización de Objetos
El universo 3D entero no es completamente observable en una pantalla 2D. Sino que solo una parte del mismo será visible, en un determinado momento, bajo una determinada posición y orientación de cámara.
La cámara mencionada anteriormente representa el ojo desde el cual se está observando el universo 3D en un determinado momento, y se la denomina Frustum. El Frustum es una figura geométrica de aspecto piramidal, que delimita la región de espacio del universo 3D que terminará siendo visible en pantalla.
Consiste en una pirámide rectangular compuesto por seis planos: near plane, far plane, left plane, right plane, top plane y bottom plane. El volumen encerrado entre estos planos dependerá de los valores configurados de la cámara: Position: lugar en el espacio en donde se encuentra la cámara, en un momento determinado
Look at: dirección hacia donde apunta la cámara en un momento determinado, partiendo desde la posición especificada anteriormente.
Near distance: distancia que existe entre la posición de la cámara y el near plane del Frustum. Indica la distancia a partir de lo cual todo empieza a ser visible. Aquello que se encuentre entre la cámara y el near plane, es decir, demasiado cerca al ojo de la cámara, no será visible.
Far distance: distancia máxima a la que un objeto será visible. Determina la posición del far plane del Frustum. Es análogo a la visibilidad máxima que puede ver el ojo.
Aspect Ratio: es relación entre el ancho y el alto de la pantalla 2D sobre la que se va a proyectar el mundo 3D. Se calcula dividiendo el ancho de la pantalla por el alto de la misma. Ratio = width / height
FOV: indica el ángulo de visión respecto del eje Y. Es lo que determina el ensanchamiento de la pirámide del Frustum, desde el near plane al far plane. Normalmente toma un valor entre 40° y 60°.
Todos los triángulos de todos los modelos del universo 3D que se encuentren dentro del volumen del Frustum serán visibles en pantalla (exceptuando aquellos que se interponen ante otros). Aquellos triángulos que se encuentran parte dentro del Frustum y parte afuera, serán recortados hasta dejar solo la parte de los mismos que es visible (triangle splitting). A este proceso de determinar que triángulos caen dentro del volumen de visión se lo denomina Frustum Culling, y puede ser realizado en distintas etapas: a nivel de la aplicación o directamente por el adaptador de video.
Una vez que se ha calculado los triángulos que se encuentran dentro del Frustum, habrá que tener en cuenta que algunos estarán tapando a otros, en lo que respecta a al ojo de la cámara. Por lo tanto no todos los triángulos dentro del Frustum terminarán convirtiéndose realmente en pixels de pantalla. A este proceso se lo denomina Occlusion Culling.
Por lo tanto el concepto de Rendering consiste en calcular, para una cámara determinada, dentro de un universo 3D determinado, que pixels deberán ser dibujados en pantalla. El proceso de Rendering es bastante complejo e involucra varias etapas.
Gracias a la existencia de APIs gráficas como OpenGL y DirectX, junto con el apoyo de los adaptadores de video, el programador normalmente no debe ocuparse de todo este proceso de transformación. Sino que se limita a especificar la geometría del mundo que quiere representar en el modelo lógico de 3D dimensiones, y luego la API gráfica en cuestión será la encargada de transformar ese mundo 3D en una matriz bidimensional de pixels.
3.3 Transformaciones Tridimensionales
Muchos de nuestros objetos del universo 3D serán estáticos, como paredes, terrenos y objetos de decoración, pero otros objetos requerirán movimiento. En 3D existen tres tipos de movimientos básicos que combinados conforman todas las alternativas necesarias. Estos movimientos se denominan transformaciones, dado que consisten en transformaciones lineales de coordenadas y son los siguientes:
·Traslación (translation): consiste en mover cada punto por una distancia constante, en una dirección específica.
·Rotación (rotation): movimiento de un objeto siguiendo una ruta circular
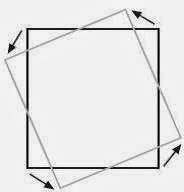
·Escalado (scaling): incrementa o disminuye el tamaño de un objeto, por un factor de escalar.
Transformation Matrix
Para aplicar cada uno de los tres movimientos a una malla compuesta por triángulos, sería necesario desplazar cada uno de los vértices de la misma al lugar correspondiente. Esta operación es engorrosa para objetos de mucha complejidad y se torna aún más complicado cuando se quieren acumular movimientos, por ejemplo: trasladarse, luego rotar y luego volver a trasladarse.
Es por ello que las APIs gráficas cuentan con una herramienta destinada a facilitar el movimiento de objetos denominada Transformation Matrix. Esta matriz tiene una estructura de 4x4:
La matriz es utilizada para representar todas las transformaciones necesarias para mover un objeto 3D en el universo. Los valores contenidos en la matriz son utilizados para mover, rotar y escalar objetos. Cada fila de la matriz representa la coordenada en el universo de cada eje. La primer fila contiene la posición del eje X, la segunda del eje Y y la tercera del eje Z. Cada elemento de la matriz representa una porción de la transformación. La matriz es inicialmente cargada con la matriz identidad.
La ventaja de almacenar los movimientos de los objetos 3D con esta matriz y no con vectores sueltos es que todos los movimientos, rotaciones y escalados a hacer a un objeto en un cuadro de animación pueden almacenarse en una sola matriz. Esto es gracias a la multiplicación de matrices.
Si queremos mover un objeto, después rotarlo y luego volverlo a mover podemos crear las matrices necesarias para cada movimiento y luego multiplicarlas todas, y así obtener una sola matriz resultante que engloba todo el movimiento completo.
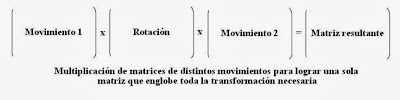
De esta forma, la API gráfica solo recibe una única matriz que representa el movimiento total de un objeto 3D en un momento determinado, y se reduce el almacenamiento de memoria requerido.
3.4 Lineas y superficies curvas
Las ecuaciones de los objetos con límites curvos se pueden expresar en forma paramétrica o en forma no paramétrica. El Apéndice A proporciona un resumen y una comparación de las representaciones paramétricas y no paramétricas. Entre los múltiples objetos son útiles a menudo en las aplicaciones gráficas se pueden incluir las superficies cuadráticas, las supercuádricas, las funciones polinómicas y exponenciales, y las superficies mediante splines. Estas descripciones de objetos de entrada se teselan habitualmente para producir aproximaciones de las superficies con mallas de polígonos.
La necesidad de representar curvas y superficies proviene de modelar objetos “from scratch” o representar objetos reales. En este último caso, normalmente no existe un modelo matemático previo del objeto, y el objeto se aproxima con “pedazos” de planos, esferas y otras formas simples de modelar, requiriéndose que los puntos del modelo sean cercanos a los correspondientes puntos del objeto real.
La representación no paramétrica de una curva (por ejemplo, en dos dimensiones) puede ser implícita, y = f(x) O bien explícita, f(x, y) = 0
La forma implícita no puede ser representada con curvas multivaluadas sobre x (por ejemplo, un círculo), mientras que la forma explícita puede requerir utilizar criterios adicionales para especificar la curva cuando la ecuación tiene más soluciones de las deseadas.
Representación paramétrica.
Una representación paramétrica (por ejemplo, de una curva bidimensional) tiene la forma P(t) = ( x(t), y(t) )T t1 <= t <= t2
La derivada o vector tangente es
P’ (t) = ( x’(t), y’(t) )T
El parámetro t puede reemplazarse mediante operaciones de cambio de variable, y frecuente se normaliza de modo que t1 = 0 y t2 = 1. Aunque geométricamente la curva aparece equivalente, una operación de este tipo normalmente modifica el comportamiento de la curva (esto es visible al comparar sus derivadas).











Comentarios
Publicar un comentario